回归模型：从理论到实践的全面指南

回归模型简介

在这个数据驱动的时代，预测和分析已成为各行各业的核心需求。从金融市场的走势预测到房地产价值评估，从能源消耗预测到个性化推荐系统，回归分析为我们提供了一个强大而优雅的数学工具，帮助我们在看似杂乱的数据中发现规律，预见未来的趋势。

核心思想

回归分析犹如在繁星密布的夜空中寻找北极星。它通过建立数学模型来揭示数据之间的内在联系，就像天文学家通过观测星象来预测天体运动。这种方法不仅能帮助我们理解已有数据的关系，更重要的是能够对未知的情况做出科学的预测。

应用场景

让我们通过一些典型场景来理解回归模型的实际应用价值：

1. 房地产市场分析
   • 输入特征：地理位置、建筑面积、房龄、周边配套等
   • 预测目标：房屋市场价值
   • 应用价值：为购房者提供价值参考，协助开发商制定精准定价策略
2. 电商销量预测
   • 输入特征：历史销售数据、节假日信息、促销活动、季节因素
   • 预测目标：未来一段时间的商品销量
   • 应用价值：优化库存管理，制定科学的营销策略
3. 个性化广告投放
   • 输入特征：用户画像、浏览历史、点击行为
   • 预测目标：广告点击率
   • 应用价值：提升广告投放效率，优化营销资源分配
4. 智慧能源管理
   • 输入特征：历史用电数据、天气预报、节假日信息
   • 预测目标：未来用电量
   • 应用价值：实现智能调度，降低运营成本

线性回归：优雅而强大的基石

线性回归是机器学习领域中最基础也最优雅的模型之一。它通过建立特征与目标之间的线性关系，帮助我们理解和预测现实世界中的各种现象。这种方法不仅计算高效，而且具有极强的可解释性。

数学原理解析

让我们以浅显易懂的方式来理解线性回归的数学本质：

1. 简单线性回归

   y = wx + b
   

   这个公式蕴含着优雅的因果关系：

   • y：我们期望预测的目标变量（如房价）
   • x：我们观察到的特征变量（如面积）
   • w：特征的权重系数（反映面积对房价的影响程度）
   • b：基准值（即使面积为0，房产也具有的基础价值）
2. 多元线性回归

   y = w₁x₁ + w₂x₂ + ... + wₙxₙ + b
   

   这是考虑多个影响因素时的扩展形式：

   • 每个x代表一个特征维度（面积、位置、房龄等）
   • 每个w表示对应特征的影响权重
   • b仍然代表基准值

最小二乘法：寻找最优参数

最小二乘法是线性回归中最经典的参数估计方法，它通过最小化预测值与实际值之间的平方误差来找到最优的模型参数。

工作原理

1. 误差计算
   • 对每个数据点，计算预测值与实际值的差异
   • 将这些差异的平方求和，得到总体误差
2. 参数优化
   • 通过求导找到使误差最小的参数值
   • 这个过程可以得到闭式解，无需迭代优化
3. 数学表达

   Loss = Σ(y_pred - y_true)² = Σ(wx + b - y)²
   

参数调整策略

1. 权重更新
   • 计算损失函数对w的偏导数
   • 沿着梯度的反方向调整参数
2. 偏置更新
   • 计算损失函数对b的偏导数
   • 同样沿梯度反方向调整

代码实战：房价预测示例

让我们通过一个实际的房价预测案例来实践线性回归：

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

# 准备示例数据：房屋面积(平方米)和价格(万元)
X = np.array([[50], [75], [100], [125], [150]])  # 房屋面积
y = np.array([100, 150, 200, 250, 300])          # 对应价格

# 创建并训练模型
model = LinearRegression()
model.fit(X, y)

# 预测新房屋的价格
new_area = np.array([[175]])  # 预测175平方米房屋的价格
predicted_price = model.predict(new_area)
print(f"175平方米房屋的预测价格: {predicted_price[0]:.2f}万元")

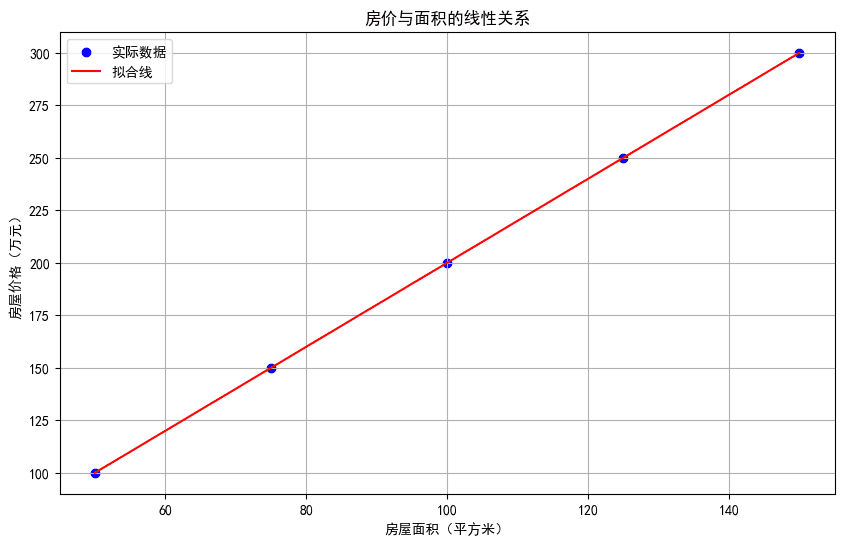
# 可视化结果
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X, model.predict(X), color='red', label='拟合线')
plt.xlabel('房屋面积（平方米）')
plt.ylabel('房屋价格（万元）')
plt.title('房价与面积的线性关系')
plt.legend()
plt.grid(True)
plt.show()

处理非线性关系：多项式回归

现实世界中的关系往往不是简单的线性关系。例如，随着房屋面积的增加，价格可能呈现加速增长的趋势。这时，我们可以引入多项式特征：

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline
import numpy as np

# 准备非线性数据
X = np.array([[50], [75], [100], [125], [150]])
y = np.array([100, 200, 400, 700, 1000])  # 价格呈现加速增长

# 创建多项式回归模型
degree = 2  # 使用二次多项式
polyreg = make_pipeline(PolynomialFeatures(degree), LinearRegression())
polyreg.fit(X, y)

# 预测新值
new_area = np.array([[175]])
pred_price = polyreg.predict(new_area)
print(f"175平方米房屋的预测价格: {pred_price[0]:.2f}万元")

应对过拟合：Ridge回归

当模型考虑过多特征时（如房屋面积、年代、楼层、朝向、装修等），容易出现过拟合现象。Ridge回归通过引入L2正则化项来解决这个问题：

from sklearn.linear_model import Ridge

# 创建Ridge回归模型
ridge = Ridge(alpha=1.0)  # alpha控制正则化强度
ridge.fit(X, y)

# 预测房价
predictions = ridge.predict(new_area)
print(f"使用Ridge回归的预测价格: {predictions[0]:.2f}万元")

特征选择：Lasso回归

在特征众多的情况下，Lasso回归可以帮助我们筛选出最重要的特征：

from sklearn.linear_model import Lasso

# 创建Lasso回归模型
lasso = Lasso(alpha=1.0)
lasso.fit(X, y)

# 进行预测
predictions = lasso.predict(new_area)
print(f"预测值: {predictions[0]}")

# 分析特征重要性
feature_importance = pd.DataFrame({
    'feature': ['面积', '年代', '楼层', '朝向', '装修'],
    'importance': abs(lasso.coef_)
})
print("特征重要性排序：")
print(feature_importance.sort_values('importance', ascending=False))

高维数据集的适用性分析

在处理高维数据集时，我们需要通过多个角度来评估线性回归的适用性：

主成分分析（PCA）

PCA可以帮助我们：

• 降低数据维度
• 发现主要特征组合
• 可视化高维数据分布

from sklearn.decomposition import PCA

# 应用PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_scaled)

# 分析主成分解释的方差比例
print("各主成分解释的方差比例：")
print(pca.explained_variance_ratio_)

t-SNE可视化

t-SNE能够保持数据的局部结构，帮助我们：

• 观察数据分布
• 发现潜在的簇
• 识别异常点

from sklearn.manifold import TSNE

# 应用t-SNE
tsne = TSNE(n_components=2, random_state=42)
X_tsne = tsne.fit_transform(X_scaled)

# 可视化结果
plt.scatter(X_tsne[:, 0], X_tsne[:, 1])
plt.title('t-SNE可视化')
plt.show()

变量关系分析

相关性分析

使用相关系数矩阵来分析变量间的线性关系：

# 计算相关系数矩阵
correlation_matrix = df[features].corr()

# 可视化相关性矩阵
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm')
plt.title('特征相关性矩阵')
plt.show()

散点图矩阵

通过散点图矩阵直观展示变量间的关系：

# 绘制散点图矩阵
sns.pairplot(df[features + ['价格']])
plt.suptitle('特征间的关系可视化')
plt.show()

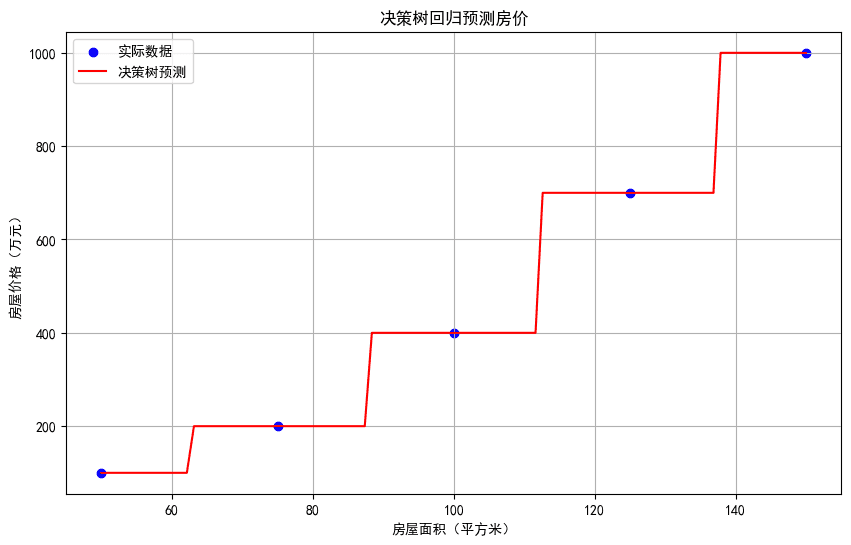
决策树回归：直观而灵活

决策树回归通过构建一个树形结构来进行预测，每个节点代表一个决策规则。这种方法特别适合处理非线性关系和类别特征。

代码实践

from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt

# 创建并训练决策树模型
regressor = DecisionTreeRegressor(max_depth=3)  # 限制树的深度，防止过拟合
regressor.fit(X, y)

# 预测并可视化
X_test = np.linspace(X.min(), X.max(), 100).reshape(-1, 1)
y_pred = regressor.predict(X_test)

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X_test, y_pred, color='red', label='决策树预测')
plt.xlabel('房屋面积（平方米）')
plt.ylabel('房屋价格（万元）')
plt.title('决策树回归预测房价')
plt.legend()
plt.grid(True)
plt.show()

随机森林：集体智慧的力量

随机森林就像是召集了一群经验丰富的房产评估师，每个人根据自己的经验给出评估，最后取平均值作为最终预测。这种”集体智慧”的方法往往能得到更稳定、更准确的结果。

代码实现

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor

# 准备非线性数据
X = np.array([[50], [75], [100], [125], [150]])
y = np.array([100, 200, 400, 700, 1000])  # 价格呈现加速增长

# 创建随机森林模型
rf_model = RandomForestRegressor(
    n_estimators=100,    # 使用100个决策树
    max_depth=None,      # 允许树充分生长
    min_samples_split=2, # 分裂所需的最小样本数
    min_samples_leaf=1,  # 叶节点最小样本数
    random_state=42
)

# 训练模型
rf_model.fit(X, y)

# 分析特征重要性
feature_importance = pd.DataFrame({
    'feature': ['面积'],
    'importance': rf_model.feature_importances_
}).sort_values('importance', ascending=False)

print("特征重要性排序：")
print(feature_importance)

plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='实际数据')
plt.plot(X_test, y_pred, color='red', label='决策树预测')
plt.xlabel('房屋面积（平方米）')
plt.ylabel('房屋价格（万元）')
plt.title('随机森林回归预测房价')
plt.legend()
plt.grid(True)
plt.show()

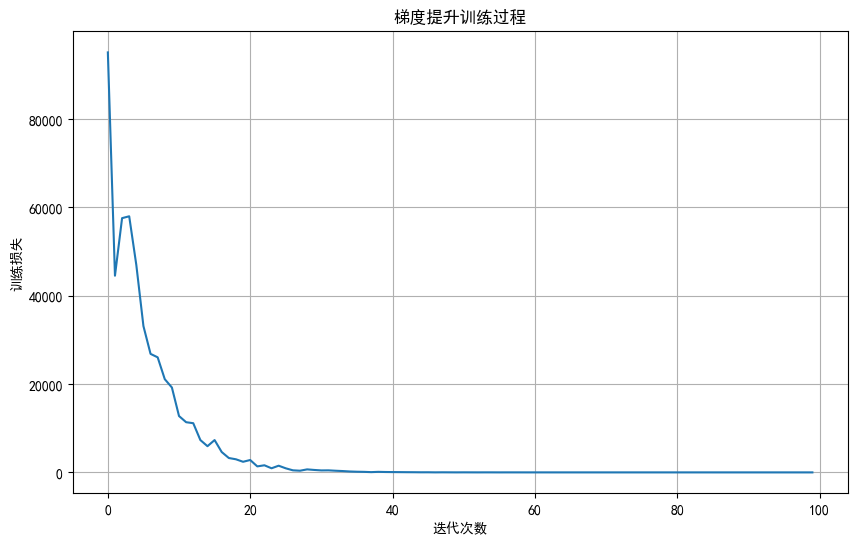
梯度提升：渐进式优化

梯度提升机（GBM）采用迭代优化策略，每次训练都专注于纠正前面模型的误差。这种渐进式的学习方法往往能够获得极高的预测精度。

代码示例

from sklearn.ensemble import GradientBoostingRegressor

# 创建GBM模型
gbm = GradientBoostingRegressor(
    n_estimators=100,   # 迭代次数
    learning_rate=0.1,  # 学习率
    max_depth=3,        # 树的深度
    subsample=0.8,      # 使用80%的样本训练每棵树
    random_state=42
)

# 训练模型并分析学习过程
gbm.fit(X, y)

# 可视化训练过程
plt.figure(figsize=(10, 6))
plt.plot(gbm.train_score_)
plt.xlabel('迭代次数')
plt.ylabel('训练损失')
plt.title('梯度提升训练过程')
plt.grid(True)
plt.show()

支持向量机回归：寻找最优边界

支持向量机回归（SVR）通过在高维空间中构建最优化边界来进行预测，特别适合处理复杂的非线性关系。

实践示例

from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler

# 数据标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
y_scaled = scaler.fit_transform(y.reshape(-1, 1)).ravel()

# 创建SVR模型
svr = SVR(
    kernel='rbf',     # 使用RBF核函数
    C=100,           # 正则化参数
    epsilon=0.1,     # 误差容忍度
    gamma='scale'    # 核函数参数
)

# 训练模型
svr.fit(X_scaled, y_scaled)

# 预测并还原结果
y_pred = svr.predict(scaler.transform(X_test))
y_pred = scaler.inverse_transform(y_pred.reshape(-1, 1)).ravel()

模型评估与选择

评估指标

在回归问题中，我们主要关注以下评估指标：

1. 均方根误差（RMSE）
   • 直观反映预测的平均偏差
   • 单位与目标变量相同，便于理解
2. 平均绝对误差（MAE）
   • 预测的平均绝对偏差
   • 对异常值不敏感
3. R²得分
   • 反映模型解释数据变异的程度
   • 值越接近1表示预测越准确

from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
import numpy as np

def evaluate_model(y_true, y_pred, model_name):
    rmse = np.sqrt(mean_squared_error(y_true, y_pred))
    mae = mean_absolute_error(y_true, y_pred)
    r2 = r2_score(y_true, y_pred)
    
    print(f"\n{model_name}评估结果:")
    print(f"均方根误差 (RMSE): {rmse:.2f}万元")
    print(f"平均绝对误差 (MAE): {mae:.2f}万元")
    print(f"R²得分: {r2:.4f}")

模型选择决策流程

在选择合适的回归模型时，需要综合考虑以下因素：

1. 数据特征
   • 数据量的规模
   • 特征的维度
   • 特征间的关系（线性/非线性）
2. 预测要求
   • 预测精度的要求
   • 模型解释性的需求
   • 预测速度的要求
3. 实际约束
   • 计算资源的限制
   • 部署环境的要求
   • 维护成本的考虑

模型选择建议

1. 简单场景，特征较少
   • 优先选择线性回归
   • 数据呈现非线性趋势时使用多项式回归
2. 特征较多，需要特征选择
   • 使用Lasso回归或Ridge回归
   • 关注特征重要性分析
3. 复杂非线性关系
   • 决策树适合处理类别特征
   • 随机森林提供更稳定的预测
   • SVR适合处理高维特征
4. 大规模数据集
   • 梯度提升机性能优越
   • 随机森林可并行训练

实战案例：房价预测系统

让我们通过一个完整的房价预测案例来综合运用各种回归模型：

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# 加载房产数据
# df = pd.read_csv('house_data.csv')

# 特征工程
# features = ['面积', '位置评分', '房龄', '楼层', '装修程度']
# X = df[features]
X0 = np.array([[50, 7, 20, 4, 5], [75, 4, 10, 2, 3], [100, 5, 5, 6, 2], [125, 3, 8, 4, 4], [150, 3, 15, 3, 1]])
y0 = np.array([100, 200, 400, 700, 1000])  # 价格呈现加速增长

# 将NumPy数组转换为DataFrame，并指定列名
X = pd.DataFrame(X0, columns=['面积', '位置评分', '房龄', '楼层', '装修程度'])
y = pd.DataFrame(y0, columns=['价格'])

# 数据预处理
X = X.fillna(X.mean())  # 处理缺失值
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y, test_size=0.2, random_state=42
)

# 创建模型字典
models = {
    '线性回归': LinearRegression(),
    '随机森林': RandomForestRegressor(n_estimators=100, random_state=42),
    '梯度提升': GradientBoostingRegressor(n_estimators=100, random_state=42),
    'SVR': SVR(kernel='rbf', C=100)
}

# 评估各个模型
results = {}
for name, model in models.items():
    # 训练与预测
    model.fit(X_train, y_train)
    predictions = model.predict(X_test)
    evaluate_model(y_test, predictions, name)

实践建议与注意事项

1. 数据预处理
   • 处理缺失值和异常值
   • 特征标准化或归一化
   • 处理类别型特征
2. 特征工程
   • 创建交互特征
   • 处理时间特征
   • 考虑特征组合
3. 模型调优
   • 使用网格搜索优化参数
   • 进行交叉验证
   • 注意过拟合问题
4. 部署考虑
   • 模型大小和计算效率
   • 预测延迟要求
   • 更新维护策略

总结与展望

回归分析作为机器学习中的基础工具，在现实世界中有着广泛而深远的应用。通过本文的学习，我们不仅掌握了各种回归模型的原理和实现方法，更重要的是理解了如何在实际问题中选择和应用合适的模型。

随着技术的发展，回归分析还将继续演进：

• 自动化机器学习（AutoML）的普及
• 深度学习与回归分析的深度融合
• 联邦学习在隐私保护下的分布式回归
• 实时学习与在线更新的广泛应用

这些新技术将为回归分析带来更多可能性，让我们能够更好地理解和预测这个复杂的世界。