K-means聚类算法：从原理到实践的完整指南

K-means算法简介

K-means算法是机器学习领域中最经典和实用的无监督学习算法之一，主要用于解决数据聚类问题。其核心思想是通过迭代方式将数据集划分为K个不同的簇，每个簇由其质心（中心点）来表示。这种方法既简单有效，又能够处理大规模数据集，在实际应用中广受欢迎。

算法原理

K-means算法的工作流程可以分为以下四个关键步骤：

1. 初始化：随机选择K个数据点作为初始质心
2. 分配：计算每个数据点到各个质心的距离，将其分配给最近的质心所在的簇
3. 更新：重新计算每个簇的质心（计算簇内所有点的均值）
4. 迭代：重复步骤2和3，直到质心位置基本不变或达到预设的迭代次数

算法特点

优点：

• 实现简单，易于理解和部署
• 计算效率高，适合处理大规模数据
• 聚类结果直观，便于解释和应用

局限性：

• 需要预先指定聚类数量K
• 对初始质心的选择较为敏感
• 可能陷入局部最优解
• 对非球形或不同密度的簇效果欠佳

实战示例

让我们通过一个完整的示例来展示K-means算法的应用过程。

1. 数据准备

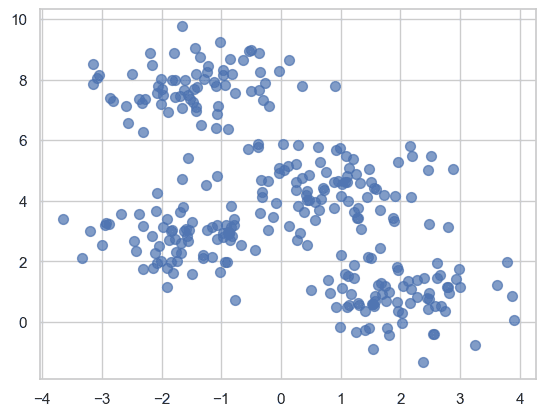
首先，我们使用scikit-learn库生成模拟数据集。这些数据点将呈现出自然的聚类趋势。

import matplotlib.pyplot as plt
import seaborn as sns

# 设置绘图风格
sns.set(style="whitegrid")

运行以下代码可以生成一系列半随机的 x 和 y 坐标对。

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成示例数据
points, cluster_indexs = make_blobs(n_samples=300, centers=4, cluster_std=0.8, random_state=0)
x = points[:, 0]
y = points[:, 1]

# 可视化原始数据
plt.scatter(x, y, s=50, alpha=0.7)
plt.title('Raw data distribution')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

2. 应用K-means算法

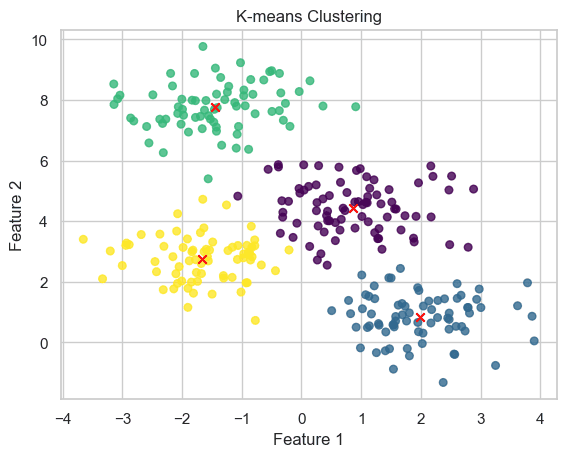
接下来，我们使用K-means算法对数据进行聚类分析，并可视化聚类结果。

import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

# 生成示例数据
points, cluster_indexs = make_blobs(n_samples=300, centers=4, cluster_std=0.8, random_state=0)
x = points[:, 0]
y = points[:, 1]

# 可视化原始数据
# plt.scatter(x, y, s=50, alpha=0.7)

# 应用K-means算法
kmeans = KMeans(n_clusters=4, random_state=0)
kmeans.fit(points)

# 获取聚类标签和中心点
labels = kmeans.labels_
centers = kmeans.cluster_centers_

# 可视化聚类结果
plt.figure(figsize=(10, 6))
plt.scatter(x, y, c=labels, s=30, alpha=0.8, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, linewidths=3)
plt.title('K-means Clustering')
plt.xlabel('Feature 1')
plt.ylabel('Feature 2')
plt.show()

3. 确定最佳聚类数量

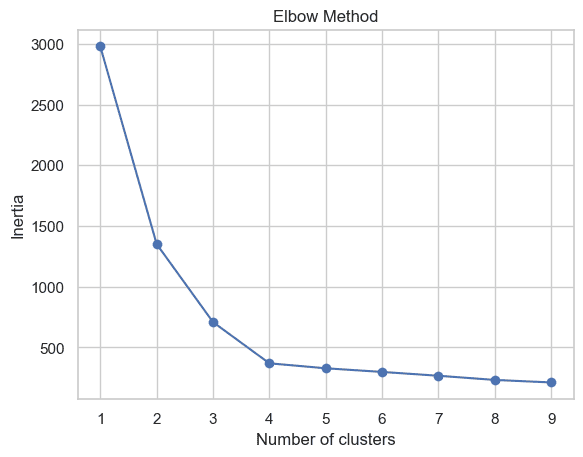
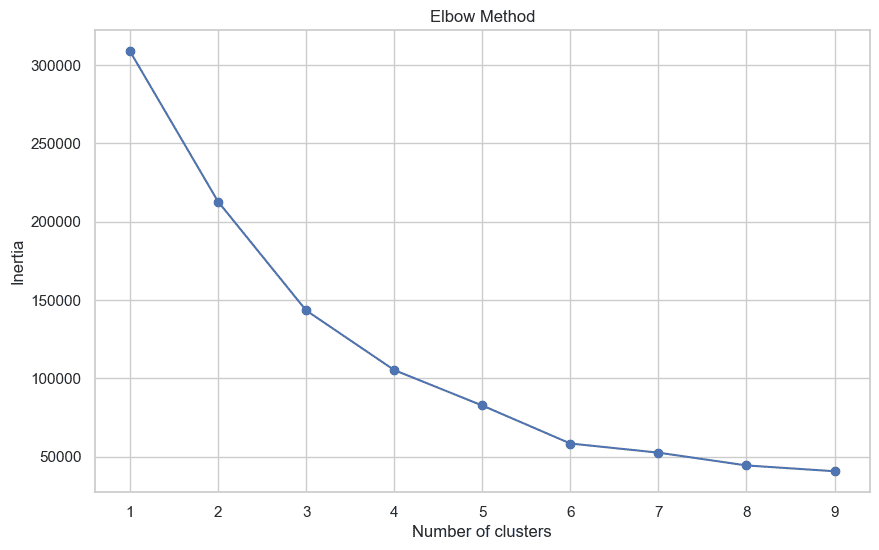
在实际应用中，如何选择合适的聚类数量K是一个关键问题。手肘法（Elbow Method）是一种常用的方法，它通过绘制不同K值对应的聚类惯性（inertia）来帮助我们做出选择。

# 计算不同K值对应的惯性
inertias = []
K = range(1, 10)

for k in K:
    kmeans = KMeans(n_clusters=k, random_state=0)
    kmeans.fit(points)
    inertias.append(kmeans.inertia_)

# 绘制手肘图
plt.figure(figsize=(10, 6))
plt.plot(K, inertias, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()

从图中可以看出，当K=4时，曲线出现明显的”肘部”，说明这可能是最佳的聚类数量。不过在实际应用中，手肘点可能并不总是那么明显，这时我们需要结合具体业务场景和其他评估指标来做出判断。

实际应用场景

K-means算法在现实世界中有着广泛的应用，例如：

• 客户分群：根据用户的消费行为、浏览习惯等特征进行市场细分
• 图像压缩：通过减少图像中使用的颜色数量来压缩图像
• 异常检测：识别与主要簇距离较远的异常数据点
• 文档聚类：将相似主题的文档组织在一起
• 传感器优化：确定传感器的最佳布置位置

1. 客户分类场景

对客户细分，以确定哪些客户可以作为促销目标，从而增加其购买活动。

本案例需要的数据集可以点击获取。

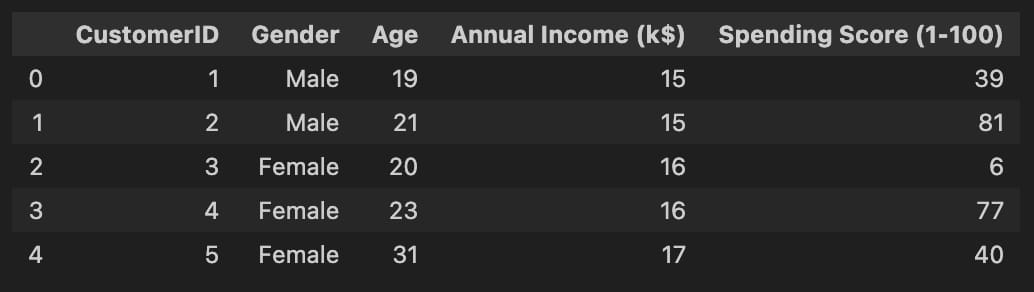
import pandas as pd

customers = pd.read_csv('data/customers.csv')
customers.head()

import matplotlib.pyplot as plt

points = customers.iloc[:, 3:5].values
x=points[:, 0]
y=points[:, 1]

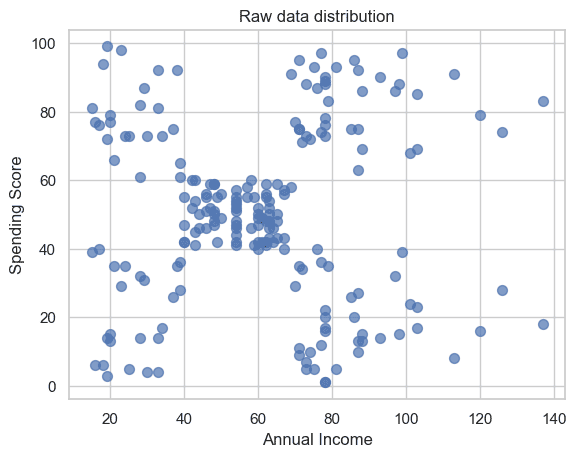
plt.scatter(x, y, s=50, alpha=0.7)
plt.title('Raw data distribution')
plt.xlabel('Annual Income')
plt.ylabel('Spending Score')
plt.show()

from sklearn.cluster import KMeans

kmeans = KMeans(n_clusters=5, random_state=0)
kmeans.fit(points)
labels = kmeans.labels_
centers = kmeans.cluster_centers_
plt.figure(figsize=(10, 6))
plt.scatter(x, y, c=labels, s=30, alpha=0.8, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', marker='x', s=200, linewidths=3)
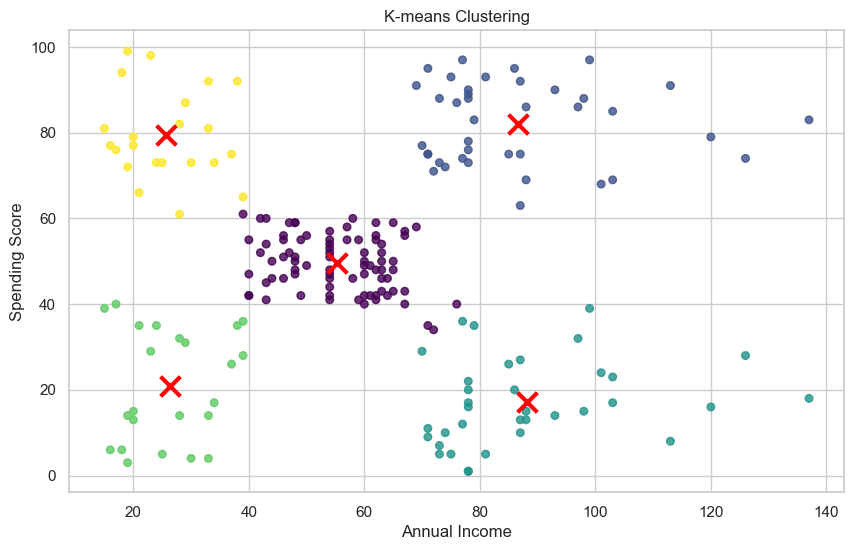
plt.title('K-means Clustering')
plt.xlabel('Annual Income')
plt.ylabel('Spending Score')
plt.show()

右下角的客户可能是我们营销的目标客户，能通过促销来增加他们的消费。因为他们收入高，但消费水平很低。

1.1 单一维度的客户分类

使用以下语句创建一个新的 DataFrame，并在起重工添加一个名为 Cluster 的列来包含聚类的索引。

df = customers.copy()
df['Cluster'] = kmeans.predict(points)
# df.head()

cluster = kmeans.predict([[120, 20]])[0]

# 过滤属于指定聚类的客户
clustered_df = df[df['Cluster'] == cluster]
clustered_df.head()

1.2 多维度的客户分类

上面的案例只使用了年收入和消费分数2个维度，下面我们尝试引入更多维度。

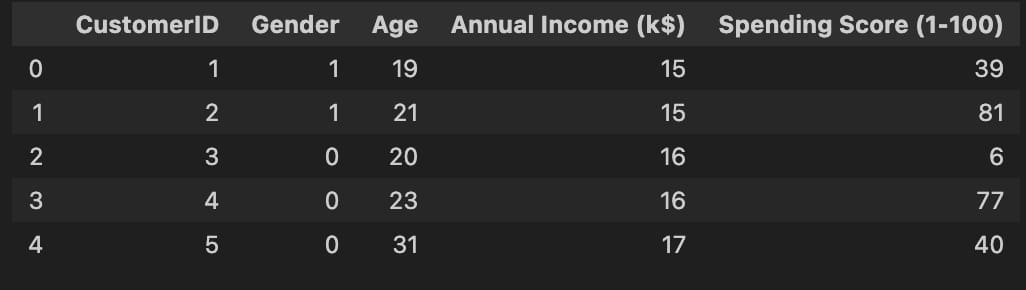
首先，我们用0和1替换Gender列中的Male和Female字符串，这个过程成为“标签编码”。这样做的原因是机器学习只能处理数字数据。

from sklearn.preprocessing import LabelEncoder

df = customers.copy()
encoder = LabelEncoder()
df['Gender'] = encoder.fit_transform(df['Gender'])
df.head()

point = df.iloc[:, 1:5].values
inertias = []

K = range(1, 10)

for k in K:
    kmeans = KMeans(n_clusters=k, random_state=0)
    kmeans.fit(point)
    inertias.append(kmeans.inertia_)

plt.figure(figsize=(10, 6))
plt.plot(K, inertias, marker='o')
plt.title('Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
plt.show()

从上图不难发现，将客户分类为5类或者6类最合适。

keams = KMeans(n_clusters=5, random_state=0)
kmeans.fit(points)

df['Cluster'] = kmeans.predict(points)
df.head()

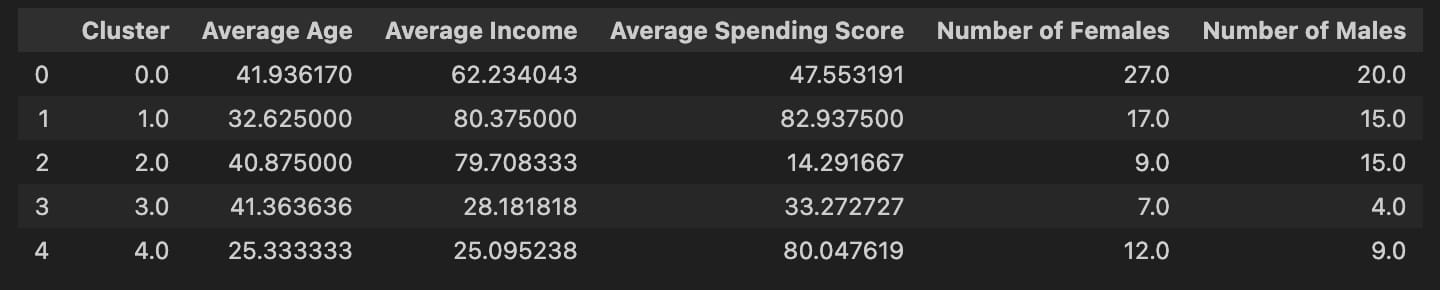
由于维度较多，不能在二维坐标中直观呈现，因此我们可以获得每个聚类中的这些坐标点距离聚类中心点的平均值，以此度量分类效果。

results = pd.DataFrame(columns=['Cluster', 'Average Age', 'Average Income', 'Average Spending Score', 'Number of Females', 'Number of Males'])

for i, center in enumerate(kmeans.cluster_centers_):
    clustered_df = df[df['Cluster'] == i]
    age = clustered_df['Age'].mean()
    income = clustered_df['Annual Income (k$)'].mean()
    spending_score = clustered_df['Spending Score (1-100)'].mean()
    females = clustered_df[clustered_df['Gender'] == 0].shape[0]
    males = clustered_df[clustered_df['Gender'] == 1].shape[0]
    
    results.loc[i] = ([i, age, income, spending_score, females, males])
    
results.head()

最后，让我们一起思考一些问题：

• 如果公司打算针对高收入但消费分数低的顾客进行促销，你会选择哪一组？
• 如果以男性或者女性作为目标呢？
• 如果目标是建立一个针对消费分数高的客户提供奖励的忠诚度计划呢？

小结

K-means算法是一种简单而强大的聚类方法，通过本文的讲解和示例，相信你已经掌握了它的基本原理和使用方法。在实际应用中，建议：

1. 根据数据特点和业务需求谨慎选择聚类数量K
2. 多次运行算法以避免局部最优解
3. 结合其他评估指标来验证聚类效果
4. 注意数据的预处理和特征工程

本文的完整代码示例可以点击获取。